树的二三事(三)
BBST平衡二叉搜索树
1、AVL树
AVL树是1962年G.M. Adelson-Velsky发明的，是第一个BBST(平衡二叉搜索树)算法
其特点很鲜明简单，就是 任意节点的左右子树高度差的绝对值不超过1 ，在Insert和Remove操作时如有必要(发生不平衡)需要对树进行重平衡。
AVL的平衡也非常简单，无非分为单旋平衡，以及双旋平衡。
但是AVL的平衡重构却是AVL树的一个很大问题，其Insert算法可以在 O(1) 复杂度实现，但是Remove算法可能达到o(logn)，在一次动态操作后，全树拓扑结构变化量可能达到 O(logn)
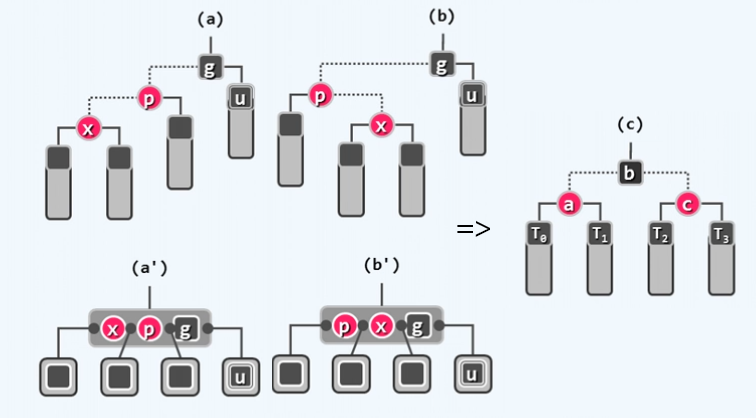
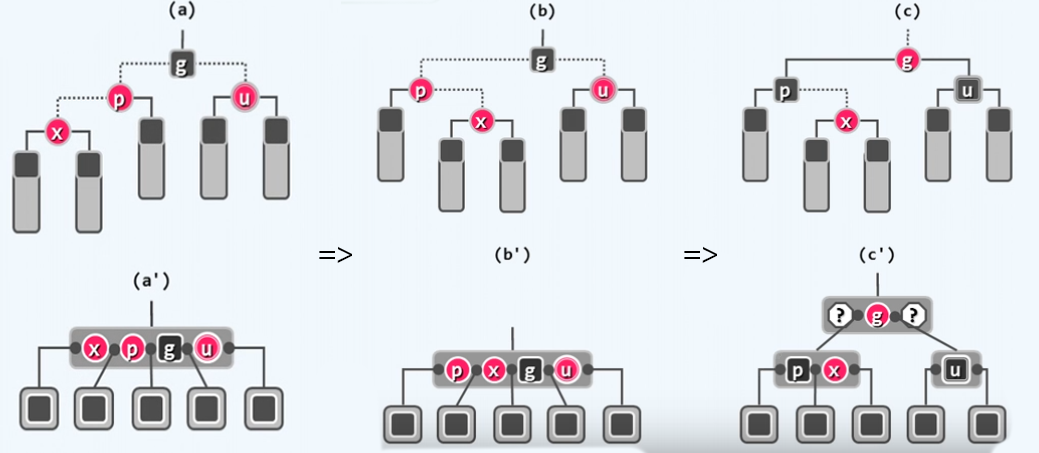
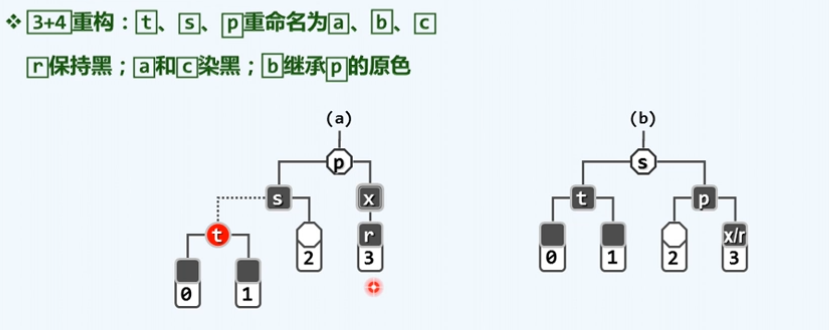
这里引入一个3+4重构算法，3+4重构算法是用于将树进行旋转的一种算法，从破而后立的思想，从目的入手。
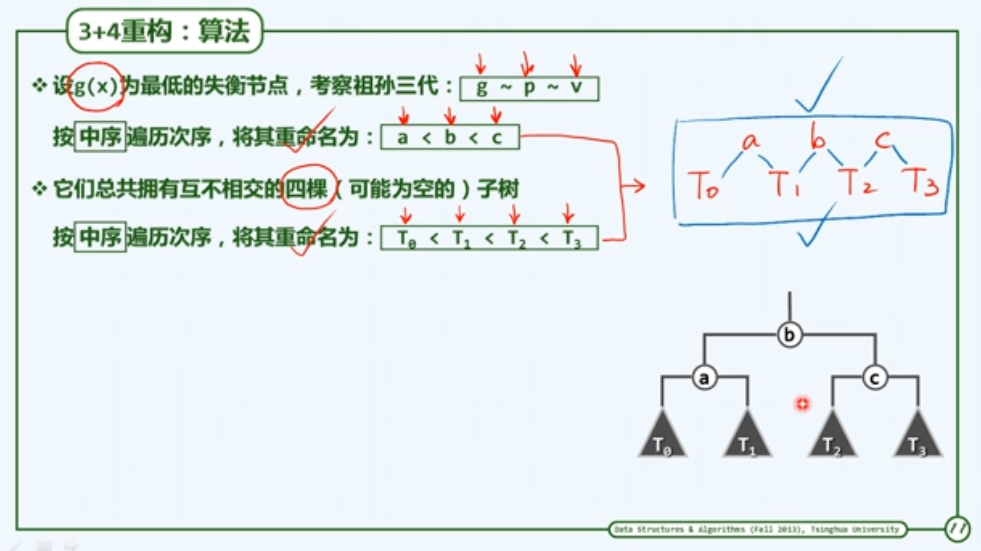
只要将祖父孙三代按照zigzig,zagzag,zigzag,zagzig,在rotateAt算法中分辨，后依次填入3+4重构算法，即可非常明了的完成旋转操作。
关于AVL和3+4重构看以下视频:
3+4重构算法视频
2、B-树
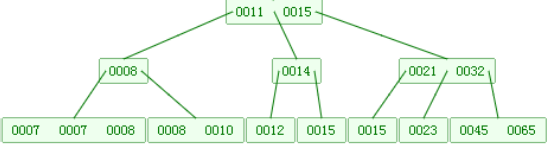
B-树有许多的变种，这里说的是最基础的B-树，B-树的设计初衷是适用于文件搜索中，因为在计算机系统中，往往制约计算过程的不是计算性能，而是IO性能，因此如何减少的IO次数就是B-树的设计理念。
B-树的每个节点不仅仅可以存储一个key-value，上限是由定义这棵树的属性决定，所有B-树又称(M/2,M)树，
意味着每个节点存储的key-value个数应当大于等于M/2且小于M，即 M/2<=COUNT<M
而且由此我们可以得出任意节点其中的kv个数等于其子节点的个数-1
- 当等于M时则需要发生分裂(上溢:节点中间的kv上移，其余分裂为两个部分，上移动kv成为两部分的粘合剂)
- 当小于M/2则需要发生合并(下溢:粘合剂下移，粘合两部分)
之所以如此设计是因为IO时我们拿1B和1KB是完全相同的时间，因此减少IO，一次取比较合适(也不能太多)，可以较好的提升性能
关于B树的动态静态操作看以下视频:
B树视频
3、红黑树
红黑树是为了解决AVL树平衡的复杂度太高的问题，实现O(1)的重构效率
红黑树的构建规则为
- 根节点为黑色
- 外部节点均为黑色(外部节点为原叶节点空着的子节点所添加上去的不存在的NULL节点)
- 若为内部节点，则红色节点的子节点只能是黑色
- 外部节点到达根: 途中的黑色结点个数相等
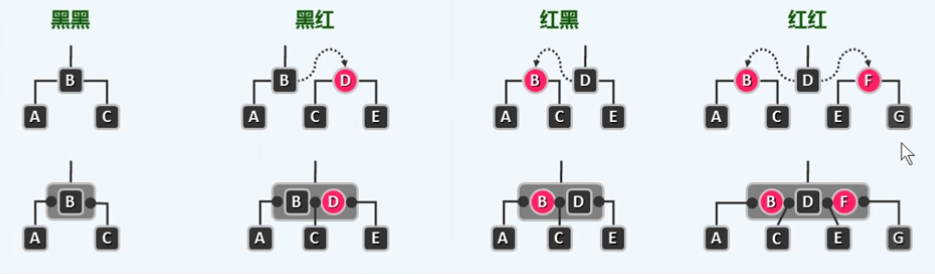
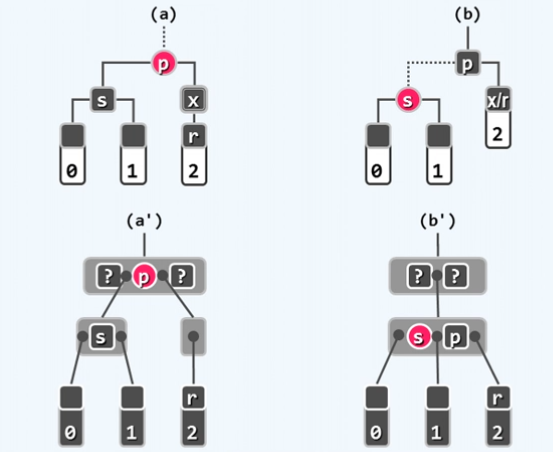
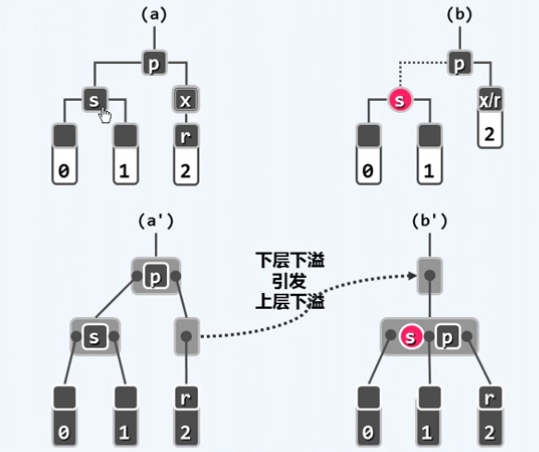
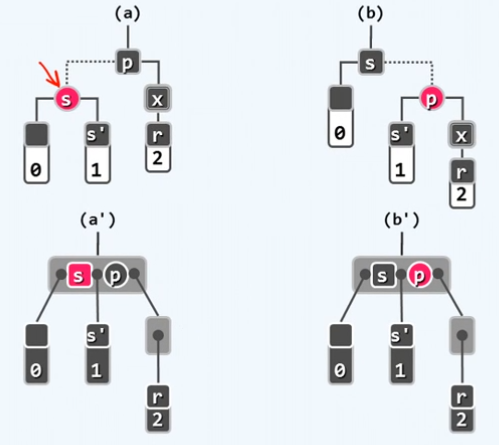
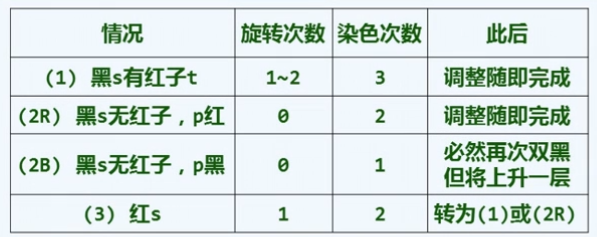
红黑树 插入 一个节点会 将其染红 因此很有可能发生双红缺陷(违反规则3)，相反删除一个节点则很容易发生双黑缺陷，因为删除了可能是一个黑色节点，导致 违反规则4
红黑树与B树的关系，两个红节点上移后不能相邻，否则发生双红缺陷
缺陷修复
红黑树在动态操作后可能会发生双红缺陷(违反规则3)，以及双黑缺陷(违反规则4)
修复各种情况的算法视频在这里:红黑树
双红缺陷 X是刚刚被插入
- 双红缺陷1=>3+4重构＋染色
-
双红缺陷2=>1次旋转+染色
双黑缺陷 X会被删除
- BB1 3+4重构+染色
- BB2R 染色(隐含的B树下溢)
- BB2B 染色(隐含的B树下溢,且可能发生持续下溢)
- BB3 旋转染色，进而转至BB1或者BB2R的情况
这里给出双黑缺陷各种情况的复杂度，可以看出无论旋转或者染色都能在O(1)时间内满足，解决了AVL的缺陷
