树的二三事(二)
一、树的多种分身
| 类型 | 内容 |
|---|---|
| 二叉树 | 二叉树· 二叉搜索树 (BST) · 笛卡尔树 · Splay Tree · Link Cut Tree · Top Tree · T树 |
| 自平衡二叉查找树 | AA树 · AVL树 · 红黑树· 伸展树· 树堆 ·节点大小平衡树 |
| B树 | B树· B+树 · B*树 · Bx树 ·UB树 · 2-3树 · 2-3-4树 ·(a,b)-树 · Dancing tree · H树 |
| Trie | 前缀树 · 后缀树· 基数树 |
| 空间划分树 | 四叉树· 八叉树· k-d树 · vp-树 · R树 · R*树 · R+树 · X树 · M树 · 线段树· 希尔伯特R树 · 优先R树 |
| 非二叉树 | Exponential tree ·Fusion tree ·区间树 ·PQ tree ·Range tree ·SPQR tree ·Van Emde Boas tree |
| 其他类型 | 堆 · 散列树 ·Finger tree ·Metric tree ·Cover tree ·BK-tree ·Doubly-chained tree ·iDistance ·Link-cut tree ·树状数组 |
二、二叉树
1、二叉搜索树(BST)
二叉搜索树BST比较简单,给出其定义及特点即可。
假设有一个二叉搜索树T,给定任意任意节点N,都满足N大于其左子节点,小于其右子节点
基于这个特征,BST的中序遍历即是节点Value从小到大的遍历
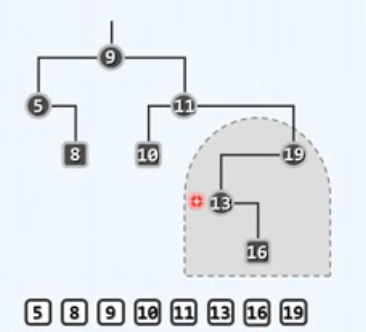
2、笛卡尔树Cartesian Tree
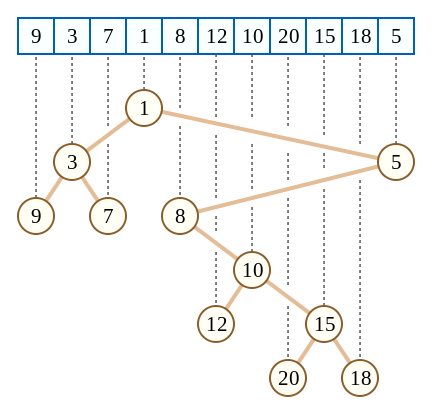
笛卡尔树是一种特殊的二叉搜索树,其有两个特征
1. 任意节点的秩均大于左子节点的秩,小于右子节点的秩
2. 任意节点的值均小于其子节点的值
性质一等同于将其秩作为构建条件,满足了二叉搜索树BST的特点(BST用值作为构建条件),将笛卡尔树中序遍历的结果
即是其用于构建时的原数组。
性质二等同于小顶堆的特点。
引入笛卡儿积的构建过程:
1. 从第一个元素开始,从左往右遍历数组L
2. 将第一个元素作为树的根节点R
3. for i in [a[1], a[2]…a[n]]
4. 如果a[i]小于其根节点R,则将a[i]作为根节点R的父节点(R成为a[i]的左子树,类似于zig旋转)
5. 如果a[i]大于其根节点R,则将a[i]从根节点的右节点开始寻找位置(未到达外部节点的临界,遵循步骤4,若到达外部节点临界仍大于当前比较节点,则成为其右子节点)
引入笛卡尔树的应用:
HDU 1506
A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.
Input
The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1 <= n <= 100000. Then follow n integers h1, …, hn, where 0 <= hi <= 1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.
Output
For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.
Sample Input
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0
Sample Output
8 4000
Solve:
构建完笛卡尔树,计算每一个节点的左右子树宽度((当前节点秩-min(左子树各节点秩))+(max(右子树个节点秩)-当前节点秩)+1)*当前节点的Value
即
S=((R-MIN(lr))+(MAX(rr)-R)+1)*Value
Value看作高,秩差之和看为宽
3、伸展树Splay Tree
这一Part可以去看看清华大学的邓俊辉老师的《数据结构与算法》第245P
伸展树是一种能够对最近访问进行自适应的BST树,可以理解为解决LRU问题的一种二叉搜索树,其特点无非就是一个能够将最后一次访问的节点提至根节点。
伸展树被提出来是为了解决AVL树在搜索时的不变通问题,因为在实际应用中,一个节点被访问,那么这个节点接下来被再次访问的几率很高(缓存),因此Splay树就根据这个特性,
得到了这个数据结构。
普通且低效的方法
一个节点被访问后,将通过一系列的zig和zag旋转将其提至根节点,最普通的做法是该节点与其父节点进行旋转。但这样做的效果在最坏情况下往往会导致非常频繁的旋转。
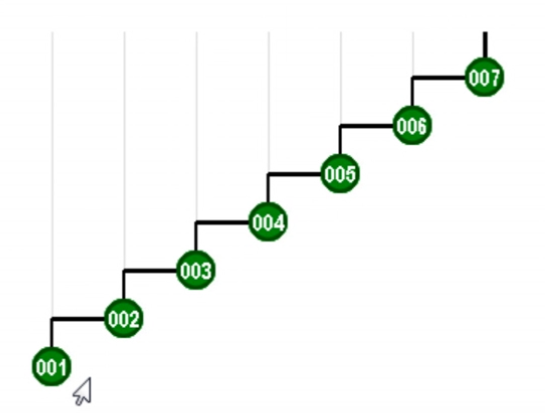
该情况通过【0,1,2,3,4,5,6,7】访问后,会发现未访问与访问后的情况一模一样,且中途进行的旋转是多余且繁琐的。
改良的方法 折叠效果 Tarjan
1.开始阶段
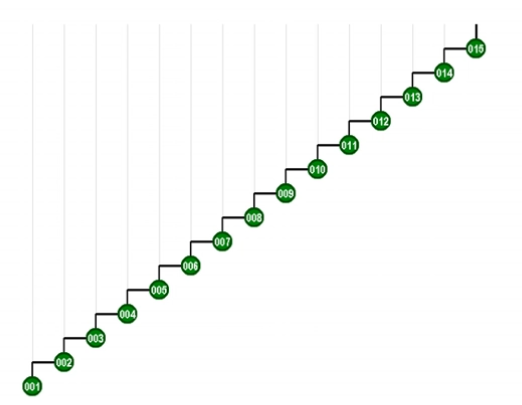
2. 旋转父与祖父节点
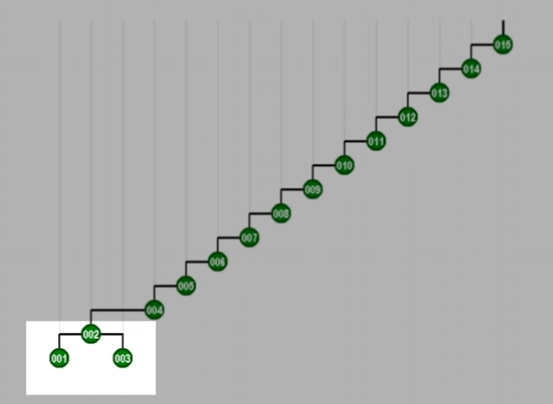
3. 旋转父子节点
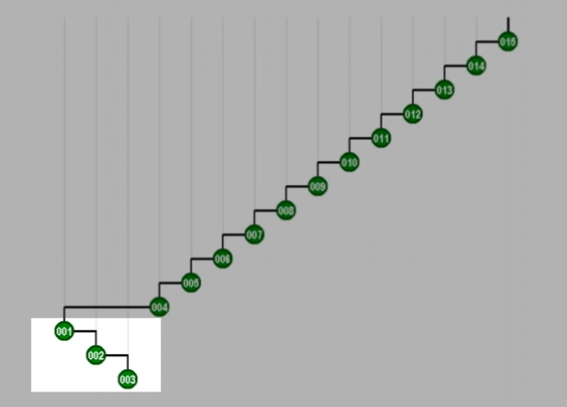
4. 重复2,3最终结果
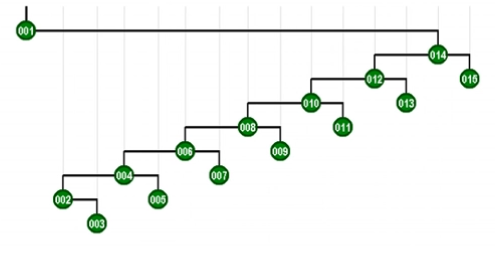
很明显树的高度降低了大约一半,虽然这一次的旋转次数不变,但意味着下一次再发送一次最深的节点访问时,不必旋转所有的节点。因此达到了优化旋转次数的效果
4、Link Cut Tree(LCT)
总结就是基于splay的一种动态树,引入了虚边、实边等概念。如果想了解,墙裂建议看👆那篇文章学习
5、Top Tree
LCT的补充